3.1.5. Решение систем алгебраических уравнений с интервальными коэффициентами методом Гаусса
Для системы линейных алгебраических уравнений
su=f (3.25)
с вещественными
коэффициентами метод Гаусса можно
описать как преобразование
исходной матрицы s к матрице
треугольного вида: ![]() и соответствующее
преобразование правых частей
и соответствующее
преобразование правых частей ![]() . При
этом
. При
этом
 ,
, 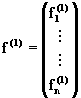 ,
,
где
![]()
![]() (3.26)
(3.26)
![]()
![]()
Вообще при ![]()
![]() и
и ![]() имеют
вид
имеют
вид
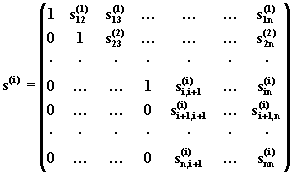 ,
, 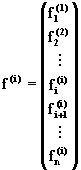
Переход от ![]() к
к ![]() , i
, i![]() n-1, осуществляется по
формулам
n-1, осуществляется по
формулам
![]()
![]()
![]() (3.27)
(3.27)
![]()
![]()
![]()
Здесь выписаны только те элементы матрицы и компоненты вектора, которые меняются при переходе. После приведения матрицы к треугольному виду решение находится из равенства
![]()
![]() (3.28)
(3.28)
Понятно, что для
возможности приведения вычислений
до конца по формулам (3.26), (3.27)
необходимо, чтобы s 11![]() 0,
0, ![]() Этого всегда можно
добиться, когда det s
Этого всегда можно
добиться, когда det s![]() 0, переставляя, если
надо, столбцы получаемых матриц (и
перенумеровывая соответствующим
образом переменные).
0, переставляя, если
надо, столбцы получаемых матриц (и
перенумеровывая соответствующим
образом переменные).
Вернемся теперь к
системе (3.24) линейных
алгебраических уравнений с
интервальными коэффициентами. В
этом случае уже нельзя говорить об
исключении неизвестных, так как,
A/A![]() 0 при w
(A)>0. Однако по
аналогии с вещественным случаем
можно преобразовать S к треугольному виду
0 при w
(A)>0. Однако по
аналогии с вещественным случаем
можно преобразовать S к треугольному виду ![]() по
формулам (3.26), (3.27), заменяя в них
вещественные коэффициенты
интервалами, а вещественные
арифметические операции -
интервально - арифметическими:
по
формулам (3.26), (3.27), заменяя в них
вещественные коэффициенты
интервалами, а вещественные
арифметические операции -
интервально - арифметическими:
![]()
![]() (3.29)
(3.29)
![]()
![]()
![]()
![]()
![]() (3.30)
(3.30)
![]()
![]()
![]()
После этого вычисляем интервалы
![]()
![]() (3.31)
(3.31)
Формулы (3.29) - (3.31) дают интервальный вариант метода Гаусса.
Из основной теоремы 3.1 интервальной арифметики непосредственно вытекает справедливость следующего утверждения :
Теорема 3.4. Пусть
интервалы Ui, i=![]() определены формулами
(3.29) - (3.31) (то есть в формулах (3.29) -
(3.31) не встречается деление на
интервал, содержащий нуль). Тогда
для любых sОS,
fО F решение
определены формулами
(3.29) - (3.31) (то есть в формулах (3.29) -
(3.31) не встречается деление на
интервал, содержащий нуль). Тогда
для любых sОS,
fО F решение ![]() системы
(7) существует, единственно и
системы
(7) существует, единственно и
![]()
Другими словами,
det s![]() 0 " sО S и
0 " sО S и
![]()
Таким образом, если мы можем с помощью (машинной) интервальной арифметики провести до конца вычисления (на ЭВМ) методом Гаусса, то можно утверждать, что то же самое справедливо для любой вещественной системы, коэффициенты и правые части которой лежат в соответствующих интервалах.
В связи со
сказанным возникает интересный
вопрос. Пусть det s![]() 0 " s ОS.
Всегда ли можно в таком случае
провести до конца вычисления
интервальным методом Гаусса? Ответ отрицательный.
Рассмотрим соответствующий пример.
0 " s ОS.
Всегда ли можно в таком случае
провести до конца вычисления
интервальным методом Гаусса? Ответ отрицательный.
Рассмотрим соответствующий пример.
Пример 3.10 (Райхмана [109]). Рассмотрим интервальную матрицу
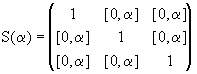 .
.
Проводя вычисления интервальным методом Гаусса, последовательно получим
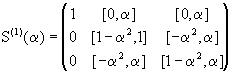 ,
,
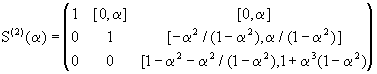 .
.
Если ![]() -
(единственный) корень уравнения (1-x2)2-x
2=0 из интервала
(0,1), то при x *
-
(единственный) корень уравнения (1-x2)2-x
2=0 из интервала
(0,1), то при x *![]() a<1
имеем 0О[1-a 2-a2/(1- a2),
1+a3/(1-a2)] и мы не можем
закончить вычисления методом
Гаусса.
a<1
имеем 0О[1-a 2-a2/(1- a2),
1+a3/(1-a2)] и мы не можем
закончить вычисления методом
Гаусса.
Возьмем a =0,62>![]() и
покажем, что для любой матрицы sОS(0,62) dets
и
покажем, что для любой матрицы sОS(0,62) dets![]() 0. Матрица
имеет вид
0. Матрица
имеет вид
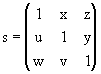 ,
,
(x, y, z, u, v, w)О D = [0, 0.62]![]() [0, 0.62]
[0, 0.62]![]() [0, 0.62]
[0, 0.62]![]() [0, 0.62]
[0, 0.62]![]() [0, 0.62]
[0, 0.62]![]() [0, 0.62]
[0, 0.62]
и ее определитель det s = 1 + wxy + uvz + wz - ux - yv = f( x, y, z, u, v, w ). Выполняя несложные, но громоздкие выкладки, нетрудно найти f(x, y, z, u, v, w) >0 при всех (x, y, z, u, v,w) О D. Итак, изложенный пример показывает, что при переходе от обычного метода Гаусса к интервальной версии свойства его, вообще говоря, ухудшаются. Результаты проведенных некоторыми авторами экспериментальных расчетов на ЭВМ также показали, что ширина вычисляемых интервалов может довольно быстро расти для систем с хорошо обусловленными матрицами. Тем не менее в случае систем с матрицами некоторых специальных видов метода Гаусса может дать (и дает) хорошие результаты. Одним из важных классов таких матриц являются M- матрицы.
Напомним, что
вещественная матрица a = (aij
)О![]() называется
М-матрицей, если aij
называется
М-матрицей, если aij![]() 0 для всех i
0 для всех i![]() j и выполнено одно из
эквивалентных условий:
j и выполнено одно из
эквивалентных условий:
1) det a ![]() 0
и a-1
0
и a-1![]() 0;
0;
2) aii>0, i=![]() , и
спектральный радиус матрицы e-d-1
a меньше единицы
(здесь e=(dij)
- единичная матрица,
d - диагональная
матрица с элементами dij = dijaij, d ij - символ Кронекера);
, и
спектральный радиус матрицы e-d-1
a меньше единицы
(здесь e=(dij)
- единичная матрица,
d - диагональная
матрица с элементами dij = dijaij, d ij - символ Кронекера);
3) все собственные значения матрицы a имеют положительные вещественные части;
4) для каждого
вектора x такого,
что ax![]() 0, имеем x
0, имеем x![]() 0.
0.
Следствие. Если
существует М - матрица b такая, что a![]() b, то a- M-матрица.
b, то a- M-матрица.
Интервальная матрица A называется M - матрицей, если M - матрицей является всякая вещественная матрица a О A.
Теорема 3.5. Пусть
S - интервальная
M-матрица,
F - неотрицательный
интервальный вектор, то есть f![]() 0 для всех fО F. Тогда
интервальный вектор можно получить
с помощью интервального метода
Гаусса, и он является оптимальным
интервальным решением системы (3.24).
0 для всех fО F. Тогда
интервальный вектор можно получить
с помощью интервального метода
Гаусса, и он является оптимальным
интервальным решением системы (3.24).
3.1.6. Интервально-аналитический метод прогонки
Рассмотрим метод прогонки для систем с трехдиагональными интервальными матрицами. Пусть о коэффициентах аi, bi, ci и правых частях fi системы
| b0 c0 0 0 0 ....................................0 | u0 | f0 | |||
| a1 b1 c1 0 0 ..................................0 | u1 | f1 | |||
| 0 a2 b2 c2 0 ..................................0 | * | u2 | = | f2 | = |
| ......................................................... | ... | .. | |||
| 0 .......................... 0 an-1 bn-1 cn-1 | un-1 | fn-1 | |||
| 0 .......................................0 0 an bn | un | fn |
известно лишь, что они принадлежат заданным интервалам :
ai О Ai, i =1, n;
bi О Bi, i = 0, n;
ci О Ci, i = 0, n-1;
fi О Fi, i = 0, n;
Тогда вместо системы (3.32) мы должны рассмотреть систему
S` U = F , (3.33)
где
| B0 C0 0 0 0 ......................................0 | ||
| A1 B1 C1 0 0 ...................................0 | ||
| 0 A2 B2 C2 0 ...................................0 | = | S |
| ............................................................ | ||
| 0 .......................... 0 An-1 B n-1 C n-1 | ||
| 0 .......................................0 0 A n B n |
есть интервальная матрица, F = (F0,F1 ,...,Fn )т — интервальный вектор, ` U — искомое решение. Запись (3.33) необходимо понимать так : требуется найти множество
` U = { u = (u0,u1,...,un) | su = f , sО S, fОF},
` Ui = { Priu | uО ` U }, i = 0,n .
Множество` U может иметь весьма замысловатую структуру. Интервально- аналитический подход позволяет отыскать интервалы Ui такие , что
` Ui![]() Ui, i = 0,n . (3.34)
Ui, i = 0,n . (3.34)
Как хорошо известно, решение системы (3.32) задается формулами
ui = xiui+1 + yi , i = n-1,n-2,...,0 (3.35)
un = yn ,
где коэффициенты xi , yi определяются соотношениями
x0 = - c0 / b0 , y0 = f0 / b0,
xi = - ci / (bi + aixi-1) , i = 1,n-1, (3.36)
yi = (fi - aiyi-1) / ( bi + aixi-1) , i = 1,n.
Покажем, что, переходя формально в формулах (3.35), (3.36) к интервалам, мы получим интервальное решение Ui .
Теорема 3.6. Пусть
Ui = XiUi+1 + Yi , i =1,n-1, (3.37)
Un = Yn,
причем Xi , Yi вычислены по формулам
Xi = - Ci / (Bi + AiXi-1) , i = 1,n-1,
X0 = - C0 / B0 , (3.38)
Yi = (Fi - AiYi-1) / (Bi + AiXi-1) , i = 1,n,
Y0 = F0 / B0, (3.39)
в которых по предположению все выражения имеют смысл. Тогда имеет место включение (3.34).
Доказательство.
Воспользуемся
основной теоремой интервальной
арифметики и методом
математической индукции. В силу
указанной теоремы, если X0, Y0 найдены из (3.36) , то x0
![]() X0 , y0
X0 , y0 ![]() Y0. Предположим, что x
i-1
Y0. Предположим, что x
i-1![]() X i-1, y
i-1
X i-1, y
i-1 ![]() Y i-1. Тогда
Y i-1. Тогда
xi = - ci / (bi + aix i-1) ![]() - Ci / (Bi + AiXi-1) = Xi ,
- Ci / (Bi + AiXi-1) = Xi ,
yi = (fi - aiy i-1) / (bi + aix i-1) ![]() (Fi - AiYi-1)/(Bi +
AiX i-1) = Yi. (3.40)
(Fi - AiYi-1)/(Bi +
AiX i-1) = Yi. (3.40)
Отсюда по индукции получаем xi ОXi, yi О Yi при всех i ; в частности, yn = un ОYn = Un. Теперь из (3.40), (3.37), (3.35) на основании теоремы 3.4 вытекает включение ui ОUi , i = n, n-1,...,0. Так как коэффициенты ai, bi, ci, fi cистемы (3.32) произвольны, отсюда следует справедливость (3.34).
Итак, формулы (3.37)-(3.38) дают интервальный вариант метода прогонки. Реализовать ее можно лишь в том случае, если в соотношениях (3.38), (3.39) не встретится деление на интервал, содержащий нуль.
3.1.7. Обращение интервальных матриц
Одним из способов решения системы уравнений (3.24) является использование обратной матрицы. Очевидно, что если нам известна матрица Т такая, что
![]() ,
,
то множество
решений системы содержится в TF: ` U ![]() TF.
TF.
Первый интервальный метод нахождения такой матрицы был предложен Хансеном. Интервальная арифметика в нем используется в комбинации с априорными оценками некоторых величин.
Выберем матрицу s* О S
(например, s* = m(S)) и вычислим
каким-либо способом матрицу t -
приближение к *![]() . Определим P
равенством P = e - St, где e - единичная
матрица. Предположим, что ||P||<1. Тогда для любой
вещественной матрицы p О P
справедливо следующее
представление:
. Определим P
равенством P = e - St, где e - единичная
матрица. Предположим, что ||P||<1. Тогда для любой
вещественной матрицы p О P
справедливо следующее
представление:
![]()
Обозначим ![]() Имеет
место неравенство
Имеет
место неравенство
![]()
Если s О S, то t -
st = p О P и, значит, ![]() , откуда
, откуда
![]() .
(3.41)
.
(3.41)
Пусть ![]() -
матрица, все элементы которой равны
-
матрица, все элементы которой равны
![]() . Из (3.41) имеем
. Из (3.41) имеем ![]() .
.
Определим интервальную матрицу Rm соотношением
Rm = ( ... ((P + e)P + e)P + ..) + e (m сложений).
Тогда ![]() для любой матрицы
s ОS.
для любой матрицы
s ОS.
Пусть теперь ![]() . -
невырожденная вещественная
матрица, а матрица
. -
невырожденная вещественная
матрица, а матрица ![]() такова, что
такова, что ![]() .
.
Рассмотрим
итеративный процесс получения
более точных интервальных
приближений к s ![]() :
:
![]() , k
>1. (3.42)
, k
>1. (3.42)
Справедливы следующие утверждения.
Теорема 3.8 :
1. Каждый член
последовательности ![]() содержит s
содержит s![]() .
.
2.
Последовательность ![]() сходится к s
сходится к s![]() тогда и только тогда,
когда спектральный радиус r(e - sm(T
тогда и только тогда,
когда спектральный радиус r(e - sm(T
![]() )) матрицы e - sm(T
)) матрицы e - sm(T ![]() ) меньше единицы.
) меньше единицы.
3. Если | | .| |монотонная
мультипликативная матричная норма [312], то для
последовательности матриц ![]() выполняется оценка
выполняется оценка
![]() ,
,
где ` w (A) - матрица с элементами w (Aij).
Пусть опять s![]()
![]() T(0) . Определим
последовательность
T(0) . Определим
последовательность ![]() равенствами
равенствами
![]() , k
>1.
, k
>1.
![]() .
(3.43)
.
(3.43)
Теорема 3.9.
1. s![]()
![]() T(
T(![]() ) при всех l =
0, 1, 2, ...
) при всех l =
0, 1, 2, ...
2.
Последовательность ![]() сходится к s
сходится к s![]() , если при
всех t
, если при
всех t ![]() T(
T(![]() )спектральный радиус
матрицы | e - st | меньше
единицы:
)спектральный радиус
матрицы | e - st | меньше
единицы:
r( | e - st |) <1. (3.44)
3. Если | | .| |- монотонная мультипликативная матричная норма, то
![]() .
.
Сформулируем
достаточно простой критерий, когда
выполняется (3.44). Пусть ![]() такова,
что s
такова,
что s![]()
![]() T и | |
e - sm(T)| |
T и | |
e - sm(T)| | ![]() 1.
Если | | ` w ( T) | | < 2(1 - | |
e - sm(T)| | ) / |
| s| |, то для всех t
1.
Если | | ` w ( T) | | < 2(1 - | |
e - sm(T)| | ) / |
| s| |, то для всех t![]() T r(| e - st | )
<1.
T r(| e - st | )
<1.
Для реализации
методов, определяемых
соотношениями (3.42), (3.43), необходимо
знать начальное приближение T(0), которое можно
получить, например, интервальным
методом Гаусса. Приведем условия,
достаточные для выполнения
включения: s![]()
![]() T.
T.
Теорема 3.10.
1. Пусть матрица ![]() такова,
что T(e - s)
такова,
что T(e - s) ![]() T - e.
Тогда s
T - e.
Тогда s![]()
![]() T.
T.
2. Если e - s -
невырожденная и матрица T такова,
что ![]() ,
то s
,
то s![]()
![]() T.
T.
3.1.8. Интервальные итерационные методы для систем линейных алгебраических уравнений
Применение
интервальных методов гарантирует
не только быструю сходимость
решения за счет обеспечения
последовательного включения
решений без особых затрат памяти
ЭВМ, но и возможность проверки
существования и единственности
решения нелинейных систем в
заданной области пространства ![]() и
сходимости соответствующих
итерационных процессов [109]. Обычные вещественные
итерационные методы типа метода
Ньютона гарантированно сходятся к
решению лишь тогда, когда начальное
приближение выбрано достаточно
близко к нему [109].
и
сходимости соответствующих
итерационных процессов [109]. Обычные вещественные
итерационные методы типа метода
Ньютона гарантированно сходятся к
решению лишь тогда, когда начальное
приближение выбрано достаточно
близко к нему [109].
Пусть система линейных алгебраических уравнений записана в виде
x = a x + b, (3.45)
![]() , причем относительно
а и b известно , что a
, причем относительно
а и b известно , что a![]() A, b
A, b![]() B,
B, ![]() .
.
В качестве примера интервальных итерационных методов для (3.45) рассмотрим метод простой итерации.
Теорема 3.11. Итерации
![]() , k
, k ![]() 0 , (3.46)
0 , (3.46)
cходятся к единственной неподвижной точке уравнения
X = A X + B
при любом
начальном ![]() тогда и только тогда, когда r
( |A| ) < 1.
тогда и только тогда, когда r
( |A| ) < 1.
Доказательство. Достаточность.Прежде всего заметим, что
`![]() .
.
Далее, поскольку r
( |A| ) < 1 и |A| ![]() 0 (0- нулевой элемент из
0 (0- нулевой элемент из ![]() ), то
), то ![]() существует и
существует и
![]()
Отсюда для
произвольных k и m ![]() 1 получаем
1 получаем
![]()
Поскольку ![]() ,
последовательность {X(k)} является
последовательностью Коши и, значит,
,
последовательность {X(k)} является
последовательностью Коши и, значит,
![]() ,
откуда X*=AX*+B.
Единственность X* следует из того,
что
,
откуда X*=AX*+B.
Единственность X* следует из того,
что
![]() .
.
Необходимость
. Пусть
итерации ![]() , сходятся к X* при любом начальном
, сходятся к X* при любом начальном ![]() . Покажем, что r (|A|) < 1.
Согласно теореме Перрона -
Фробениуса вещественная
неотрицательная матрица |A| = (|Aij|) имеет
неотрицательный собственный
вектор, соответствующий
собственному значению l = r ( |A| ).
. Покажем, что r (|A|) < 1.
Согласно теореме Перрона -
Фробениуса вещественная
неотрицательная матрица |A| = (|Aij|) имеет
неотрицательный собственный
вектор, соответствующий
собственному значению l = r ( |A| ).
Из сходимости X(k) к X*при
произвольном X(0)
следует сходимость ![]() к ` w (X*).
Выберем X (0) так,
чтобы ` w (X(0)) являлся собственным
вектором |A|, соответствующим l = r ( |A| ),
и по крайней мере один из
компонентов` w (X(0)) был больше
соответствующего компонента w (X* ).
Тогда, предположив r ( |A| )
к ` w (X*).
Выберем X (0) так,
чтобы ` w (X(0)) являлся собственным
вектором |A|, соответствующим l = r ( |A| ),
и по крайней мере один из
компонентов` w (X(0)) был больше
соответствующего компонента w (X* ).
Тогда, предположив r ( |A| ) ![]() 1, получим
1, получим
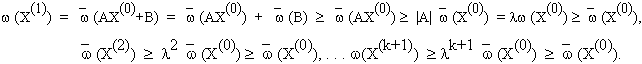
Переходя к
пределу, имеем ` w
(X*) ![]() ` w (X(0)),
что противоречит выбору X (0). Теорема доказана.
` w (X(0)),
что противоречит выбору X (0). Теорема доказана.
Нетрудно
показать, что`![]() . Кроме того Х*,
оптимально в следующем смысле: не
существует интервального вектора
. Кроме того Х*,
оптимально в следующем смысле: не
существует интервального вектора ![]() такого,
что
такого,
что ![]() .
В самом деле, из равенства X* = AX* + B
следует, что
.
В самом деле, из равенства X* = AX* + B
следует, что
![]() ,
,
где
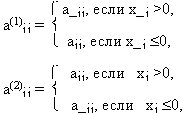
т.е. ![]() . Другими словами, х_ *,`х*
. Другими словами, х_ *,`х* ![]() { х|х=ах+b, a
{ х|х=ах+b, a ![]() A, b
A, b![]() B}.
B}.
Если мы начинаем
итерации по формуле (3.46) при
произвольном ![]() , то несмотря на
равенство
, то несмотря на
равенство ![]() , нет гарантии, что X*
, нет гарантии, что X* ![]() , а
значит, и того, что `
X
, а
значит, и того, что `
X![]() .
.
С другой стороны,
такая гарантия будет , если ![]() выбран с условием X*
выбран с условием X* ![]()
![]() . Действительно, из
монотонности по включению тогда
следует, что
. Действительно, из
монотонности по включению тогда
следует, что
![]()
и по индукции X* ![]() и X*
и X*![]() + B, а значит,
+ B, а значит,
![]() .
.
Отсюда вытекает
видоизменение алгоритма (3.46).
Выберем ![]() такое,
что
такое,
что ![]()
![]() X* , и положим
X* , и положим
![]() .
.
Из сказанного
ранее следует, что X* ![]() при всех
k = 1,2,... Если вычисления ведутся в
машиной интервальной арифметике,
то эта последовательность сходится
за конечное число шагов, т.е.
начиная с некоторого
при всех
k = 1,2,... Если вычисления ведутся в
машиной интервальной арифметике,
то эта последовательность сходится
за конечное число шагов, т.е.
начиная с некоторого ![]() , так
что выполнение равенства
, так
что выполнение равенства ![]() может служить
естественным критерием
прекращения итераций.
может служить
естественным критерием
прекращения итераций.
Еще один подход к
пострoению итерационных методов
для системы (3.24) состоит в
следующем. Умножим обе части этого
уравнения на невырожденную матрицу
Y. Например, ![]() и положим T = e - Ys. Если ||T||<1,
то возьмем вектор
и положим T = e - Ys. Если ||T||<1,
то возьмем вектор ![]() такой, что `
такой, что `![]() , и
определим последовательность
, и
определим последовательность
![]() .
(3.47)
.
(3.47)
Справедлива следующая теорема.
Теорема 3.12.Если для некоторой матрицы Y справедливо неравенство
||e - Ys|| ![]() 1,
1,
то, каковы бы ни
были s ![]() S, f
S, f ![]() F, система
имеет единственное решение и при
любом k
F, система
имеет единственное решение и при
любом k ![]() 0 это
решение содержится в интервальном
векторе U(k),
найденном с помощью (3.47).
0 это
решение содержится в интервальном
векторе U(k),
найденном с помощью (3.47).
В качестве U(0) можно взять, например, вектор с компонентами
![]() .
.
Как видно из библиографии [276]и работы [104]подавляющее большинство публикаций по линейной алгебре в интервальном анализе посвящено исследованию вопроса о решении системы интервальных уравнений
![]() (3.48)
(3.48)
где ![]() ,
, ![]() ,
, ![]() - множества
интервальных nn-матриц, n -векторов и чисел
соответственно.
- множества
интервальных nn-матриц, n -векторов и чисел
соответственно.
В интервальном анализе ищут обычно, так называемое, поточечное решение [271] системы интервальных уравнений (3.48), т.е. множество
![]() .
.
Такое понятие
поточечного решения не
удовлетворяет сложившейся
концепции решения уравнения, т.е.
подстановка найденного x* в (3.48) не дает равенства
левой и правой частей уравнений.
Соответствующее этой концепции
решение названо в [103] алгебраическим
интервальным решением ![]() , причем
, причем ![]() .
Алгоритм получения этих решений
подробно изложен в [103].
.
Алгоритм получения этих решений
подробно изложен в [103].
Существуют также
стандартные пакеты прикладных
программ по решению систем
уравнений с интервальными
матрицами коэффициентов [190]. Для линейной системы
уравнений ![]() существует интервальный
аналог метода
Ньютона-Гаусса-Зейделя ( IGS) [325]. Этот метод требует
незначительных затрат по памяти и
времени на каждом шаге, но может
медленно сходиться.
существует интервальный
аналог метода
Ньютона-Гаусса-Зейделя ( IGS) [325]. Этот метод требует
незначительных затрат по памяти и
времени на каждом шаге, но может
медленно сходиться.
Симметрические
методы [325] имеют
более высокую скорость сходимости
чем IGS. Эти
методы используют частичную
упорядоченность на ![]() .
Сходимость этих методов
доказывается с помощью
интервальной арифметики с
использованием теоремы о включении
[304].
.
Сходимость этих методов
доказывается с помощью
интервальной арифметики с
использованием теоремы о включении
[304].
Существует также
целый ряд методов, основанных на
использовании обратной матрицы ![]() .
Алефельдом и Херцбергером
предложен итеративный процесс
получения более точных
интервальных приближений к
обратной матрице [109]. Множество решений
.
Алефельдом и Херцбергером
предложен итеративный процесс
получения более точных
интервальных приближений к
обратной матрице [109]. Множество решений ![]() может
состоять из одного или нескольких
интервалов. В этом случае указанный
выше метод применяется для каждого
из этих интервалов отдельно [109].
может
состоять из одного или нескольких
интервалов. В этом случае указанный
выше метод применяется для каждого
из этих интервалов отдельно [109].
При наличии в
задаче точных исходных данных
интервальный анализ позволяет
обеспечить порождение границ и
сходимость к решению при
сравнительно слабых предложениях
[8]. Не обязательным для решения
систем линейных алгебраических
уравнений является и требование,
чтобы начальное приближение ![]() содержало в себе множество решений
линейной системы. В [109]описаны методы Румпа и
Гея, для которых это включение
достигается в ходе итераций.
содержало в себе множество решений
линейной системы. В [109]описаны методы Румпа и
Гея, для которых это включение
достигается в ходе итераций.
Современные методы интервального анализа кроме основных арифметических операций над интервальными величинами содержат развитые средства для решения систем линейных и нелинейных уравнений, методы решения дифференциальных уравнений и т.д. [48, 109, 247, 304, 323].
Целью интервального анализа при решении дифференциальных уравнений является получение строгих верхних и нижних границ решения по заданным границам (интервалам) исходных данных (начальных и граничных значений, коэффициентов уравнений и т.п.) [304]. Эти методы применимы для решения линейных и нелинейных обыкновенных дифференциальных уравнений в частных производных [247, 304] и являются более надежными, строгими и простыми по сравнению с классическими методами решения дифференциальных уравнений. Кроме того, в них автоматически учитывается неточность, связанная с ошибками округления ЭВМ.
Использование понятия интервальных ограничений и кода Hensel дало возможность [283] создать специальные методы для ЭВМ, свободные от ошибок округления и применить их для решения целого ряда приложений (решение систем линейных уравнений, интервального линейного программирования и т.д.). Наиболее подробная библиография работ по интервальной математике (около 1700 работ) содержится в обзоре [276].
Общим недостатком применения интервальных методов является наличие в некоторых случаях слишком широких интервальных оценок результата, что не всегда приемлемо для проведения практических расчетов.
[К предыдущей главе].....[К содержанию] ......[К следующей главе]